Veremos dos de los sistemas de medición de ángulos:
- sistema sexagesimal: donde la unidad de medida de ángulos es el grado
- sistema circular: donde la unidad de medida de ángulos es el radián
Sistema sexagecimal
Si la circunferencia la dividimos en 360 partes iguales, cada arco así determinado está contenido en un ángulo de amplitud un grado que escribimos 1°.
Si este arco está dividido en 60 partes iguales, cada arco resultante está contenido en un ángulo de amplitud un minuto que escribimos 1’.
Si el arco correspondiente de 1’lo dividimos en 60 partes iguales, obtenemos ángulos de amplitud un segundo que escribimos 1’’.
Por ejemplo: 10° 30’ lo podemos expresar 10,5°
Sistema circular
Cuando la medida de un arco de circunferencia TM es un radio, la medida del ángulo TOM es un radián.
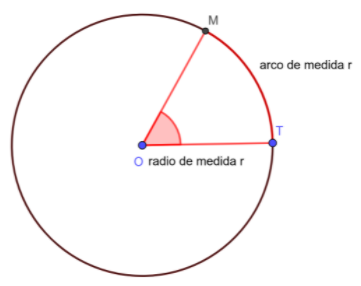
Esto significa que usamos el radio como unidad.
Es decir el radián es un ángulo al centro que abarca un arco igual al radio y su medida es por tanto 1rad.
La medida de la circunferencia es igual a 2.π.r (siendo r la medida del radio), por lo tanto se tiene que:
- la medida del arco completo es 2.π (veces) un radio
- la medida de un ángulo completo es 2.π radianes
Podemos obtener así una relación entre la medida en grados y la medida en radianes de un ángulo.
360° ______ 2.π radianes
Utilizando una regla de tres podemos pasar un ángulo de grados a radianes o viceversa.
En el siguiente applet podrás ver la definición de radián. Mueve lentamente el deslizador "deslízame" y observa. Luego ve a la retroalimentación para ver las conclusiones.
Definición: un radián es la medida del ángulo que subtiende al arco de circunferencia que tiene la misma longitud que el radio.
Entonces, como el radio de una circunferencia cabe 2π veces en el perímetro, podemos decir que en el ángulo central de la circunferencia cabrán 2π radianes. Si sabemos que el ángulo central, en grados, es de 360° y en radianes es de 2π radianes, entonces podemos deducir que:
2π rad = 360° o lo que es lo mismo πrad = 180°