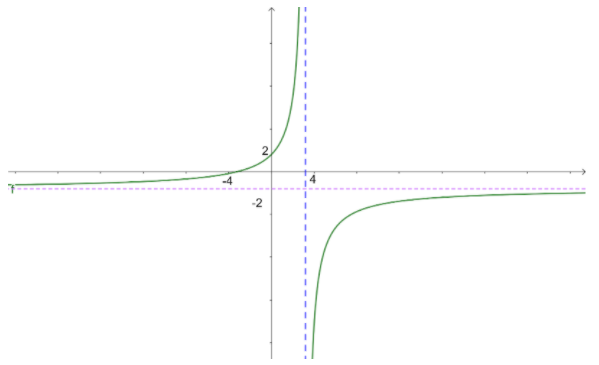
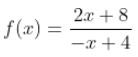Estudio de una función racional de la forma:
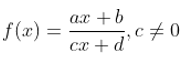
Trabajaremos lo conceptual y en paralelo iremos desarrollando un ejemplo: 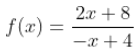
El dominio de la función es el conjunto más amplio de números reales para el cual la expresión tiene sentido. Como la división entre 0 no está definida, el dominio de la función es el conjunto de todos los números reales que no anulan al denominador. Se escribe de la siguiente manera:
![]()
Siendo ![]() la raíz del denominador, es decir que se obtiene resolviendo la ecuación: cx + d = 0
la raíz del denominador, es decir que se obtiene resolviendo la ecuación: cx + d = 0
En el ejemplo, resolvemos la ecuación: - x + 4 = 0, de donde x = 4 y escribimos:
![]()
La expresión anterior se lee, “El dominio de la función f es el conjunto de los números reales menos el 4”, quiere decir que la variable x puede tomar cualquier valor excepto el 4, porque si x = 4, veamos lo que sucede con la función en ese valor:
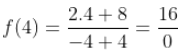
Como la división entre 0 no está definida, f(4) no se puede calcular, entonces decimos que para x =4 la función no existe.
Raíz de la función: La raíz de una función es el valor de x cuya imagen es 0. Por lo tanto para hallar la raíz debemos resolver la ecuación: f(x) = 0.
En el ejemplo:
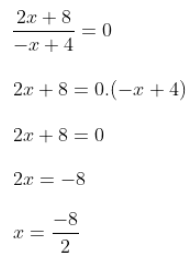
x = - 4 es la raíz de la función, para verificarlo, sustituimos la x por -4 y observamos que la imagen es 0, es decir que: f(-4) = 0
Gráficamente quiere decir que la gráfica corta el eje x en el punto de coordenadas (-4, 0).
Signo de la función racional
Estudiar el signo de una función es determinar para cada elemento del dominio si su imagen es un número positivo, negativo o cero.
Teniendo en cuenta la expresión analítica de una función racional, se puede decir que la función será positiva si el numerador y el denominador son del mismo signo y negativa si son de signos diferentes. Recordando la regla de los signos de la división de números reales. Y será cero cuando se anula el numerador sin anularse o sea sin hacerse cero el denominador. El signo de la función depende entonces del signo del numerador y del signo del denominador.
Sigamos con la función racional de expresión:
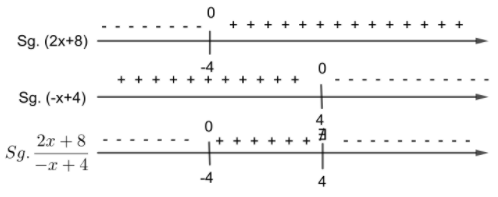
Observaciones a partir del estudio del signo:
- Para los valores de x menores a -4 y mayores que 4 las imágenes son negativas. Por ejemplo: f(-6) es negativo y f(5) es negativo
- Para los valores de x comprendidos entre -4 y 4 las imágenes son positivas. Por ejemplo: f(-3) es positivo y f(2) es positivo.
- Para el valor de x igual a -4 (como es la raíz) su imagen es cero, y escribimos f(-4) = 0
- Para el valor de x igual a 4, la función no tiene imagen, es decir no existe.
Asíntotas
En matemática, se le llama asíntota de la gráfica de una función a una recta a la que se aproxima continuamente la gráfica de tal función; es decir que la distancia entre las la gráfica y la recta es cada vez menor, es decir que tiende a ser cero (0), a medida que se extienden indefinidamente.
Las asíntotas pueden ser verticales, horizontales u oblicuas. En el estudio de las funciones racionales analizaremos la existencia de la asíntota vertical y de la horizontal. Para ello observaremos el comportamiento de la función racional en el valor de x para el cual la función no existe (VER DOMINIO) y que ocurre con la misma cuando x toma valores muy grandes o muy pequeños.
Asíntota vertical
Sigamos trabajando con el ejemplo: 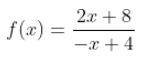
Ya habíamos escrito el dominio de esta función como: ![]()
x = 4 no tiene imagen porque no pertenece al dominio de f
Estudiaremos el comportamiento de la función para valores de x cercanos a 4.
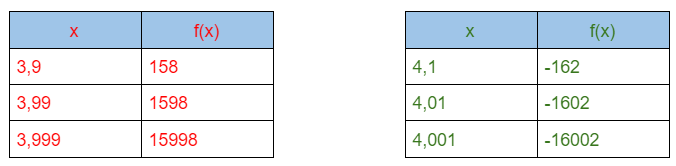
Observando las tablas de valores anteriores se concluye que:
Si los valores de x se aproximan al 4 por la izquierda, es decir por valores menores a 4 (que lo anotaremos 4-), la función toma valores positivos cada vez más grandes.
Si los valores x se aproximan al 4 pero por la derecha, es decir por valores mayores que el 4 ( que lo anotaremos 4+), la función toma valores negativos, cada vez más pequeños.
Resumiendo: Diremos que cuando x tiende a 4- la función tiende a +infinito y cuando x se acerca a 4+, la función tiende a -infinito y lo escribimos así:
![]()
La recta de ecuación x = 4 es la asíntota vertical de la gráfica de f. Intuitivamente, la gráfica “tiende a pegarse” a esa recta.
Este resultado lo representamos de la siguiente manera:
_(1).png)
Asíntota horizontal
Analizaremos el comportamiento de la función cuando x toma valores muy grandes o muy pequeños.
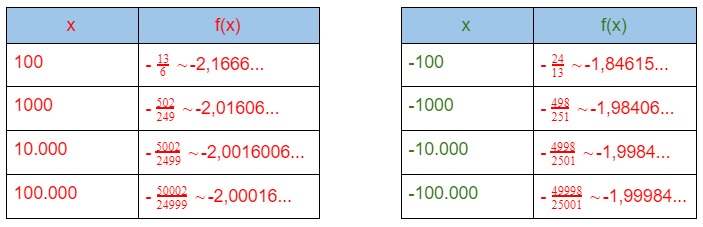
Observamos que si x tiende a +infinito la función tiende a 2 y lo mismo sucede si x tiende a -infinito.Diremos que la recta de ecuación y = 2, es asíntota horizontal a la gráfica de la función y esta “tenderá a pegarse” a dicha recta.
Este resultado lo representamos de la siguiente manera:
_(1).png)
Observación:

Representación gráfica
La gráfica corresponde a la de la función cuya expresión analítica es: