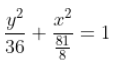Hallar la ecuación de las elipses con centro en el origen, a partir de los datos dados :
- Sus semiejes miden 5 y 2 y eje focal y = 0
- Su eje mayor mide 12, la distancia focal es de 8 y el eje focal coincidente con el eje y
- Los focos: F'(-3, 0) y F(3, 0), y su eje mayor mide 10.
- Los focos son F(2,0), F´(-2, 0) y la excentricidad igual a 23
- Los vértices V(0, 6) y V´(0, -6) y pasa por el punto (3, 2)
1.-
semieje mayor mide 5, por lo tanto a = 5
semieje mejor mide 2, por lo tanto b = 2
como el eje focal es la recta de ecuación y = 0 quiere decir que es es eje x, por lo tanto la ecuación de esta elipse es de la forma:
Sustituyendo los valores de a y b, se obtiene que la ecuación de la elipse es:
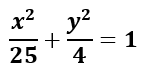
2.-
el eje mayor mide 12, por lo tanto 2a = 12, de donde a = 6
la distancia focal es 8, por lo tanto 2c = 8, de donde c = 4
Usando la relación que cumplen los parámetros: a2 = b2 + c2 , se obtiene que b = 20
Como la elipse tiene eje mayor coincidente con el eje y, la ecuación es de la forma:
Sustituyendo los valores de a y b, se obtiene que la ecuación de la elipse es:
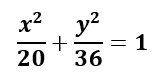
3.-
Se puede representar en los ejes para visualizar mejor su posición y elementos:
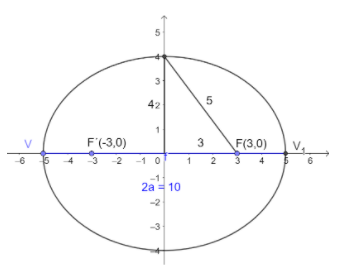
el semieje mayor: 2a = 10 a = 5
la distancia focal: 2c = 6 c = 3
el semieje menor: b2 = 25 - 9 b = 4
Ecuación:
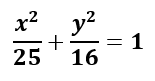
Excentricidad: e = 3/5
4.-
como la distancia focal es 4, c = 2
la excentricidad es 2/3, por lo tanto c/a = 2/3, de donde a = 3
b2 = 9 - 4
b2 = 5
La ecuación de la elipse es:
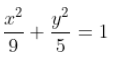
5.-
De las coordenadas de los vértice se obtiene que a = 6 y que la elipse tiene eje coincidente con el eje y, por lo tanto es de la forma:
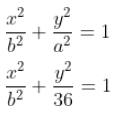
Sustituyendo las coordenadas del punto que pertenece a la elipse (3,2) y operando se obtiene:
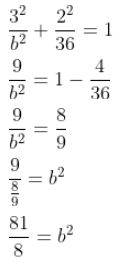
Escribimos la ecuación: