Hallar las ecuaciones de las elipses a partir de los siguientes datos:
- Centro C(1, -1), un foco en F(1, 2) y un vértice en V(1,4)
- Los focos son F(3,5) y F´(3,2) y el eje mayor es 10
1) Observando las coordenadas en x de los tres puntos, vemos que es la misma. Por lo tanto el eje mayor es vertical.
Así tenemos que: a = 5 c = 3 .
La ecuación de esta elipse es del tipo: 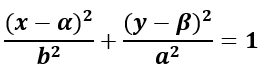
Calculamos el semieje menor: b2 = 52 - 32 b = 4
Así, la ecuación reducida de la elipse es:
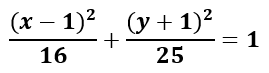
2) El centro de la elipse es el punto medio entre los focos, por lo tanto sus coordenadas son: (3, 7/2)
Como el eje mayor es 10, a = 5
De la distancia del centro a los focos, obtenemos que: c = 3/2
Usando el Teorema de Pitágoras, se calcula b, siendo b^2 = 91/4
La ecuación de la elipse es:
![]()